Eban Cardano the Third with Raku and Perl
[166] Published 23. January 2022.This is my response to the Perl Weekly Challenge #148.
Challenge #148.1: Eban Numbers
Eban Numbers <= 100.
An Eban number is a number that has no letter ‘e’ in it when the number is spelled in English (American or British).
Example:
2, 4, 6, 30, 32 are the first 5 Eban numbers.
Let us start with Perl for a change...
There are several modules on CPAN capable of doing this translation for us.
Lingua::EN::Numbers uses a traditional procedural interface, and was last updated in 2015.
File: eban-LEN-perl
#! /usr/bin/env perl
use strict;
use warnings;
use feature 'say';
use Lingua::EN::Numbers qw/num2en/;
my $limit = int($ARGV[0] || 100);
my @numbers;
for my $candidate (1 .. $limit)
{
push(@numbers, $candidate) unless num2en($candidate) =~ /e/;
}
say join(", ", @numbers);
Running it:
$ ./eban-LEN-perl
2, 4, 6, 30, 32, 34, 36, 40, 42, 44, 46, 50, 52, 54, 56, 60, 62, 64, 66
Math::BigInt::Named uses an object oriented interface, and was last updated in 2021.
File: eban-MBN-perl
#! /usr/bin/env perl
use strict;
use warnings;
use feature 'say';
use Math::BigInt::Named;
my $limit = int($ARGV[0] || 100);
my @numbers;
for my $candidate (1 .. $limit)
{
push(@numbers, $candidate)
unless Math::BigInt::Named->new($candidate)->name =~ /e/;
}
say join(", ", @numbers);
Running this version gives the same result:
$ ./eban-MBN-perl
2, 4, 6, 30, 32, 34, 36, 40, 42, 44, 46, 50, 52, 54, 56, 60, 62, 64, 66
A Raku Version
This is straight forward translation of the Perl version(s), but shorter as we can use a sequence.There are several Raku nodules doing the translation. Let us start with Lingua::Number:
The module does not pass the bundled
tests, so we have to force install it (with
zef install --force-test Lingua::Number). The module is actually broken,
so the tests should fail.
Here is the program. It does not work (on Rakudo/MoarVM v2021.12), but may do so in the future if the module is fixed:
File: eban-LN
#! /usr/bin/env raku
use Lingua::Number;
unit sub MAIN (Int $limit = 100);
(1 .. $limit).grep( { ! cardinal($_, 'en').contains('e') } ).join(", ").say;
The last line does the work. Start with the positive integers (up to the limit), get rid of values that does contain the letter «e», join them together (with commas), and print the lot.
The following REPL interaction shows that it is indeed bonkers:
> use Lingua::Number;
Nil
> cardinal(12, 'en')
> say cardinal(12, 'en')
> say cardinal(12)
> say cardinal(12121)
thousand
> say cardinal(451)
hundred
> say ordinal(451)
hundred
The Lingua::EN::Numbers module does work, and it has the same API:
File: eban-LEN
#! /usr/bin/env raku
use Lingua::EN::Numbers;
unit sub MAIN (Int $limit = 100);
(1 .. $limit).grep( { ! cardinal($_).contains('e') } ).join(", ").say;
Running it:
$ ./eban-LEN
2, 4, 6, 30, 32, 34, 36, 40, 42, 44, 46, 50, 52, 54, 56, 60, 62, 64, 66
The Lingua::NumericWordForms module has a slightly different API:
File: eban-LNWF
#! /usr/bin/env raku
use Lingua::NumericWordForms;
unit sub MAIN (Int $limit = 100);
(1 .. $limit).grep( { ! to-numeric-word-form($_).contains('e') } ).join(", ").say;
Running it gives the expected result:
$ ./eban-LNWF
2, 4, 6, 30, 32, 34, 36, 40, 42, 44, 46, 50, 52, 54, 56, 60, 62, 64, 66
Challenge #148.2: Cardano Triplets
5 Cardano Triplets.
A triplet of positive integers (a,b,c) is called a Cardano Triplet if it satisfies the below condition.
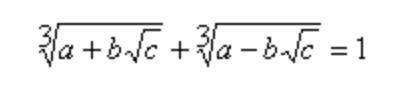
Example:
(2,1,5) is the first Cardano Triplets.
The expression «first» is vague. Do we report the first values
we get (from whatever scheme we cook up to get them) - or the ones with the lowest values for
a, b and c. And what do I mean with «lowest values»? The
sum, or what?
The Math::Root module gives us a cube root function.
Let us dive in, and see how that goes:
File: cardano-triplets-1
#! /usr/bin/env raku
use Math::Root;
unit sub MAIN (Int $count = 5, :v(:$verbose)); # [1]
my $ct := gather # [2]
{
for 1 .. Inf -> $a # [3]
{
for 1 .. Inf -> $b # [3a]
{
for 1 .. Inf -> $c # [3b]
{
say ": Considering $a, $b, $c" if $verbose;
take ($a, $b, $c) # [4]
if root($a + $b * root($c), 3) + root($a - $b * root($c), 3) == 1;
}
}
}
}
$ct[^$count].map({ say "(" ~ @$_.join(", ") ~ ")" if $_ }); # [5]
[1] Specify another limit than 5, if you feel like it.
[2] Setting up the sequence of triplets with
gather/take is ideal here.
[3] Iterate over the three variables, a, b and c.
[4] Return (so to spreak) the triplet with take, if it satisfies
the equation.
[5] Print the result, one triplet on each line. The postfix if test
skips undefined values, if we do not have the requested number (i.e.
$count) og triples.
The program runs forever, without any output.
Verbose mode to the rescue:
$ ./cardano-triplets-1 -v
: Considering 1, 1, 1
: Considering 1, 1, 2
: Considering 1, 1, 3
: Considering 1, 1, 4
It hangs on 1,1,4. Let us see why, in REPL:
> use Math::Root;
Nil
> root(1 - 1 * root(4), 3)
It hangs on that one (the second part of the expression in [4]).
The expression can be shortened to:
> root(-1,3)
Which also hangs. It should give -1, as -1 * -1 * -1 = -1.
Let us have a go at another module. BigRoot, this time in REPL to see if it works:
> use BigRoot
> BigRoot.newton's-root(root => 3, number => -1)
Constraint type check failed in binding to parameter '$number';
expected BigRoot::PositiveNumber but got Int (-1) …
This is not good.
But hey, we can work around this, by removing the sign - if negative - and add it back in to the result.
File: cardano-triplets-2
#! /usr/bin/env raku
use Math::Root;
unit sub MAIN (:$count = 5, :v(:$verbose));
my $ct := gather
{
for 1 .. Inf -> $a
{
for 1 .. Inf -> $b
{
for 1 .. Inf -> $c
{
my $left = $a + $b * root($c);
my $right = $a - $b * root($c);
say ": Considering $a, $b, $c" if $verbose;
take ($a, $b, $c) if cube-root($left) + cube-root($right) == 1;
}
}
}
}
$ct[^$limit].map({ say "(" ~ @$_.join(", ") ~ ")" if $_ });
sub cube-root ($number)
{
return root($number, 3) if $number >= 0;
return - root(- $number, 3);
}
Running it:
...
: Considering 1, 1, 4428
: Considering 1, 1, 4429
: Considering 1, 1, 4430
: Considering 1, 1, 4431
: Considering 1, 1, 4432
: Considering 1, 1, 4433
^C
Oops!
It goes on forever, in the inner loop. So I had to stop the program.
Let us add a reasonable upper limit to the previously infinite loops. The chosen default value of 21 is the result of trial and error.
File: cardano-triplets-3
#! /usr/bin/env raku
use Math::Root;
unit sub MAIN (Int :$limit = 21, :$count = 5, :v(:$verbose));
my $ct := gather
{
for 1 .. $limit -> $a
{
for 1 .. $limit -> $b
{
for 1 .. $limit -> $c
{
my $left = $a + $b * root($c);
my $right = $a - $b * root($c);
say ": Considering $a, $b, $c" if $verbose;
take ($a, $b, $c) if cube-root($left) + cube-root($right) == 1;
}
}
}
}
$ct[^$count].map({ say "(" ~ @$_.join(", ") ~ ")" if $_ });
sub cube-root ($number)
{
return root($number, 3) if $number >= 0;
return - root(- $number, 3);
}
Running it with increased limit values (showing that the if-test in the
print statement has a purpose):
$ ./cardano-triplets-3 -limit=10
(2, 1, 5)
$ ./cardano-triplets-3 -limit=15
(2, 1, 5)
(5, 2, 13)
$ ./cardano-triplets-3 -limit=20
(2, 1, 5)
(5, 2, 13)
(17, 9, 20)
(17, 18, 5)
$ ./cardano-triplets-3 -limit=21
(2, 1, 5)
(5, 2, 13)
(8, 3, 21)
(17, 9, 20)
(17, 18, 5)
Perl
This is a straight forward translation of the last Raku version. File: cardano-triplets-perl
#! /usr/bin/env perl
use strict;
use warnings;
use feature 'say';
use feature 'signatures';
use Getopt::Long;
no warnings qw(experimental::signatures);
my $verbose = 0;
my $limit = 21;
my $count = 5;
GetOptions("limit" => \$limit, "count" => \$count, "verbose" => \$verbose);
for my $a (1 .. $limit)
{
for my $b (1 .. $limit)
{
for my $c (1 .. $limit)
{
my $left = $a + $b * sqrt($c);
my $right = $a - $b * sqrt($c);
say ": Considering $a, $b, $c" if $verbose;
if (cube_root($left) + cube_root($right) == 1)
{
say "($a, $b, $c)";
$count--;
last if $count == 0;
}
}
}
}
sub cube_root ($number)
{
return $number ** (1/3) if $number >= 0;
return - ( (-$number) ** (1/3) ); # [1]
}
[1] Instead of cube roots, we can do this.
Running it:
$ ./cardano-triplets-perl
(8, 3, 21)
(17, 9, 20)
(17, 18, 5)
Oops. The first two matches are missing. That is caused by rounding errors, which Rako does not have. Here is an example:
$ perl -e "print (1/3) * 3"
0.333333333333333
$ raku -e "print (1/3) * 3"
1
Using e.g. the Math::BigFloat module should fix the problem, at the cost of cumbersome syntax:
File: cardano-triplets-MBF-perl
#! /usr/bin/env perl
use strict;
use warnings;
use feature 'say';
use feature 'signatures';
use Getopt::Long;
use Math::BigFloat;
no warnings qw(experimental::signatures);
my $verbose = 0;
my $limit = 21;
my $count = 5;
GetOptions("limit" => \$limit, "count" => \$count, "verbose" => \$verbose);
for my $a (1 .. $limit)
{
for my $b (1 .. $limit)
{
for my $c (1 .. $limit)
{
my $left = Math::BigFloat->new($a);
my $right = Math::BigFloat->new($a);
my $c_sqrt = Math::BigFloat->new($c)->bsqrt;
$left->badd(Math::BigFloat->new($b)->bmul($c_sqrt));
$right->bsub(Math::BigFloat->new($b)->bmul($c_sqrt));
say ": Considering $a, $b, $c" if $verbose;
my $sum = cube_root($left)->badd(cube_root($right));
if ($sum->beq(1))
{
say "($a, $b, $c)";
exit if $count-- == 1;
}
}
}
}
sub cube_root ($number)
{
my $third = Math::BigFloat->new(1)->bdiv(3);
return $number->bpow($third) unless $number->is_negative; # include zero.
return $number->babs()->bpow($third)->bneg();
}
Running it gives this result, after about 6 minutes:
$ ./cardano-triplets-MBF-perl
(5, 2, 13)
(8, 3, 21)
(17, 18, 5)
Still only three values, but not the same as before.
I give in.
An Observation About «First»
The triple(1,21,21) (given an upper limit of 21) will come before
(2,1,1) the way that i have programmed this (with triple for loops).
We should perhaps consider the second one as a better match first-wise,
than the first. I have no idea how to go about generating such a sequence, though.
And that's it.